문제
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
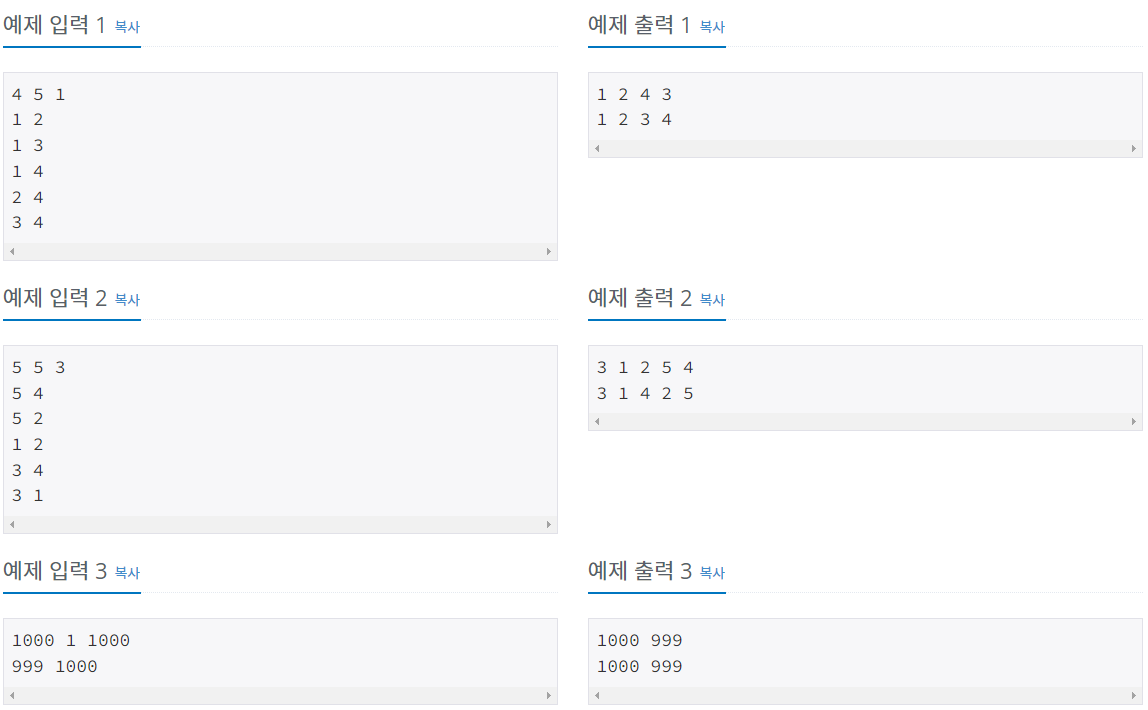
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
답안
from collections import deque
def dfs():
ST = []
visited = [0] * (N+1)
ST.append(V)
answer = []
while ST:
val = ST.pop()
if not visited[val]:
visited[val] = 1
answer.append(val)
for i in sorted(G[val], reverse=True):
if not visited[i]:
ST.append(i)
print(*answer)
# dfs
# N+1 크기의 배열을 만들고, 시작값(V)를 스택에 넣어준다.
# 스택이 존재하면 반복하는 반복문을 생성하고 ST의 마지막 값을 빼고 val이라는 변수로 선언
# val을 방문하지 않았다면, 방문표시를 해주고 answer에 그 값을 넣어준다.
# 숫자가 작은순서부터 방문해야 하기 때문에 내림차순으로 바꿔주고, (스택은 뒤에서부터 나가니까)
# G[val] 내부에 있는 i(val과 연결된 노드들)이 기존에 방문하지 않았다면 스택에 넣어준다.
def bfs():
Q = deque()
visited = [0] * (N+1)
Q.append(V)
answer = []
while Q:
val = Q.popleft()
if not visited[val]:
visited[val] = 1
answer.append(val)
for i in sorted(G[val],reverse=False):
if not visited[i]:
Q.append(i)
print(*answer)
# bfs
# 큐를 이용한다.
# Q의 0번째에 있는 값을 빼고 val로 선언한다.
# val을 방문하지 않았다면 방문표시 해주고 answer에 값을 넣어준다.
# G[val] 내부를 순회하고, Q는 0번째 인덱스부터 pop되기 때문에 오름차순으로 바꿔준다.
# G[val] 내부에 방문하지 않은 노드들이 있다면 방문처리 해주고 Q에 넣어준다.
N, M, V = map(int, input().split())
G = [[] for _ in range(N+1)] # 연결된 노드를 볼수있는 인접리스트 생성
for i in range(M):
v1, v2 = map(int, input().split())
G[v1].append(v2)
G[v2].append(v1)
dfs() # dfs 결과
bfs() # bfs 결과후기
깊이우선탐색인 dfs는 계속해서 자식노드 하나를 끝까지 타고들어가서, 더 이상 진행할 수 없을 때 분기점으로 돌아간다.(명확히 말하자면 돌아가는건 아니고,,, 순간이동 한다고 생각하면 될 것이다.)
너비우선탐색인 bfs는 자식노드들을 기점으로 퍼져나간다.
추후에 시간이 난다면 dfs와 bfs에 대해서 정리하는 글을 써볼까 한다.
처음 접해보는 타입의 알고리즘 유형이라 적응중이다 ㅎㅎ...
728x90
'파이썬 코딩테스트' 카테고리의 다른 글
| 백준 2178번 - 미로 탐색 (파이썬/Python) (0) | 2024.02.20 |
|---|---|
| 백준 1697번 - 숨바꼭질 (파이썬/Python) (1) | 2024.02.19 |
| 백준 2485번 - 가로수 (파이썬/Python) (0) | 2024.02.17 |
| 백준 1929번 - 소수 구하기 (파이썬/Python) (0) | 2024.02.16 |
| 백준 1978번 - 소수 찾기 (파이썬/Python) (0) | 2024.02.15 |



